Home Up Greg Warrington: Research

Research


Interests: My interests are algebraic combinatorics (Kazhdan-Lusztig polynomials, combinatorics of Weyl groups, and diagonal harmonics)
and gerrymandering
CV: PDF format
Gerrymandering:
  1. Evaluations of gerrymandering metrics using simulated packing and cracking
    In preparation.
  2. Packed voters and cracked voters (Version 2; Aug 03, 2018)
    In revision.
  3. Accumulation charts for instant-runoff elections
    Notices of the AMS, Dec. 2019
    Zoomable demo of chart
    Source code for interactive charts
  4. A comparison of partisan-gerrymandering measures (Version 2; Nov 04, 2018)
    code here
    Elec. Law J., 18(3), 2019.
  5. Introduction to the declination function for gerrymanders
    Friendly introduction to Elec. Law J. Quantifying gerrymandering... paper.
  6. Gerrymandering and the net number of US House seats won due to vote-distribution asymmetries (also on arXiv)
    Joint with J. Buzas.
    This will be split into two papers, one on simulated packing and cracking, other on Chen-Cottrell paper.
    Guest post on Rick Hasen's Election Law Blog.
  7. Quantifying gerrymandering using the vote distribution (older version on arXiv)
    Election Law Journal, 17 (1)
    gzipped tar file of python code used to generate data in ELJ paper
    Declination in Federal district court opinion for Ohio case (Householder v. Ohio A. Philip Randolph Institute)
  8. Other resources
    • Python code to compute the declination.
    • R code to compute the declination.
    • Report on California Redistricting Commission by Eric McGhee utilizing the declination.
    • 30-second introduction:
      The declination is essentially the angle between the two black lines.
      The bigger the angle, the more partisan asymmetry. Click below to enlarge.
      Declination examples
    • Click the image for animation from 1972 to 2016
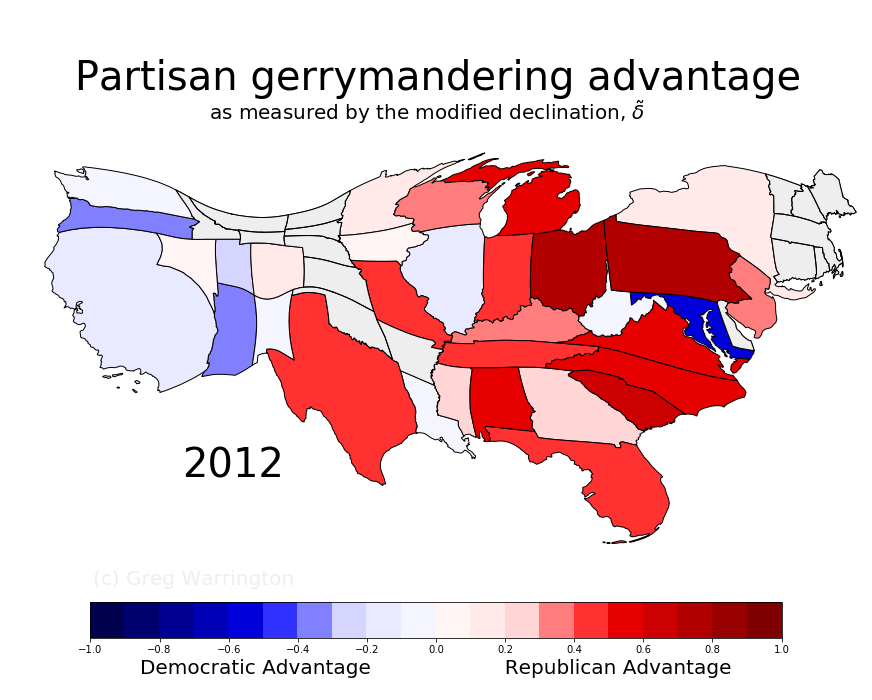
      Cartogram of partisan advantage for 2012
      Notes on the animation:
      • The cartogram adjusts state sizes according to the number of congressional seats.
        The sizes used are based on the sizes of the 2012 congressional declinations.
      • The version of the declination used is one (delta tilde) that is essentially independent of the number of seats.
        • The 2003 Texas redistricting is striking.
      • States without at least one seat won by each party are in gray.
      • Sorry Don Young and HI, you didn't fit.
Combinatorics.
  1. Abacus histories and the combinatorics of creation operators
    Joint with N. Loehr.
    In revision.
    Python and SageMath code to accompany paper:
  2. Quasisymmetric and Schur expansions of cycle index polynomials
    Joint with N. Loehr.
    Discrete Mathematics, 342 (1), January 2019, 113--127.
    Sage worksheet for computations in the paper. also as a text file
  3. Orthogonal bases for transportation polytopes applied to Latin squares, magic squares and Sudoku boards
    Linear Algebra Appl., 531, October 2017, 285--304.
    Sage worksheet for constructing bases described in the paper.
  4. Sweep maps: A continuous family of sorting algorithms
    Joint with D. Armstrong and N. Loehr
    Sage worksheet for checking various conjectures described in the paper.
    Advances in Mathematics, 284 (2015), 159-85.
  5. Rational parking functions and Catalan numbers
    Joint with D. Armstrong and N. Loehr
    Sage worksheet for checking various conjectures described in the paper.
    Annals of Combinatorics, 20 (1), March 2016, 21--58.
  6. Shape and pattern containment of separable permutations
    Joint with A. Crites and G. Panova
    Ars Combinatoria, Volume CXXVIII, July, 2016, 103--116.
  7. Martin Gardner's minimum no-three-in-a-line problem
    Joint with A. Cooper, O. Pikhurko and J. Schmitt
    American Mathematical Monthly, 121:3 (2014), 213-221.
  8. Transition matrices for symmetric and quasisymmetric Hall-Littlewood polynomials
    Joint with N. Loehr and L. Serrano
    Journal of Combinatorial Theory, Series A, 120:8 (2013), 1996-2019.
    Sage worksheet for computing various matrices described in the paper.
  9. On the existence of three dimensional Room frames and Howell cubes
    Joint with J. Dinitz and E. Lamken
    Discrete Math, 313:12 (2013), 1368-1384. Find it here.
  10. What to expect from a game of Memory
    Joint with D. Velleman
    American Mathematical Monthly, 120:9 (2013), 787-805.
  11. Quasisymmetric expansions of Schur-function plethysms
    Joint with N. Loehr
    Proceedings of the AMS, 140 (2012), 1159--1171.
  12. Equivalence classes for the mu-coefficient of Kazhdan-Lusztig polynomials in S_n
    Experimental Math., 20 (2011), no. 4, 457--466.
  13. The Spectra of Certain Classes of Room Frames: The Last Cases
    Joint with J. Dinitz
    Elec. J. Combin. 17 (2010), no. 1, Research Paper 74, 13 pp.
  14. From quasisymmetric expansions to Schur expansions via a modified inverse Kostka matrix
    Joint with E. Egge and N. Loehr
    European J. Combin. 31 (2010), no. 8, 2014--2027.
  15. A combinatorial version of Sylvester's four-point problem
    Adv. in App. Math., 45 (2010) no. 3, 390--394.
  16. A continuous family of partition statistics equidistributed with length
    Joint with N. Loehr
    J. Combin. Theory Ser. A 116 (2009), no. 2, 379--403. (final version)
  17. Nested quantum Dyck paths and nabla(s_lambda)
    Joint with N. Loehr
    International Mathematics Research Notices 2008; Vol 2008: article ID rnm157 (final version)
  18. Bitableaux bases for Garsia-Haiman modules of hollow type
    Joint with E. Allen and M. Cox
    J. Combin. Theory Ser. A 115 (2008), no. 7, 1127--1155.
  19. A human proof for a generalization of Shalosh B. Ekhad's 10^n Lattice Paths Theorem
    Joint with N. Loehr and B. Sagan
    Ars Combin. 89 (2008), 421--429.
  20. Square q,t-lattice paths and nabla(p_n)
    Joint with N. Loehr
    Transactions of the AMS, 359 (2007) no. 2, 649-669.
  21. The combinatorics of a three-line circulant determinant
    Joint with N. Loehr and H. Wilf
    Israel Journal of Mathematics 143 (2004), 141-156
  22. Juggling probabilities
    American Mathematical Monthly 112, no. 2 (2005), 105-118
  23. Counterexamples to the 0,1-Conjecture
    Joint with T. McLarnan
    Represent. Theory 7 (2003), 181-195 (final version)
  24. A formula for inverse Kazhdan-Lusztig polynomials in S_n.
    J. Comb. Theory A, Vol. 104, Iss. 2 , November (2003), 301-316 (final version)
  25. Maximal singular loci for Schubert varieties in SL(n)/B.
    Joint with S. Billey
    Trans. AMS 355 (2003), no. 10, 3915--3945 (electronic) (final version)
  26. Kazhdan-Lusztig polynomials for 321-hexagon-avoiding permuations.
    Joint with S. Billey
    J. of Alg. Comb., 13 (2): 111-136, March 2001 (final version)
Misc.:
  1. Urinary Buprenorphine, Norbuprenorphine and Naloxone Concentrations and Ratios
    Warrington, Jill S. MD, PhD; Warrington, Gregory S. PhD; Francis-Fath, Samuel BA; Brooklyn, John MD
    Journal of Addiction Medicine, ahead of print.
  2. Use of urinary naloxone levels in a single provider practice: a case study
    Jill S. Warrington, Kaitlyn Booth, (GSW), Samuel Francis-Fath
    Addiction Science and Clinical Practice, 15:3, December 2020.
  3. Predicting effects of future development on a territorial forest songbird: methodology matters
    Michelle L. Brown, Therese M. Donovan, Ruth M. Mickey, Gregory S. Warrington, W. Scott Schwenk, David M. Theobald
    Landscape Ecology 33:1 (January 2018), 93-108.
  4. Estimating landscape carrying capacity through maximum clique analysis
    Joint with Therese M. Donovan, W. Scott Schwenk and Jeffrey H. Dinitz
    Ecological Applications, 22:8 (2012), 2265-2276.
  5. A Photographic Assignment for Abstract Algebra
    PRIMUS 19 (2009), no. 6, 561-564.
Not refereed:
  1. Juggling Performers + Math = ?
    Math Horizons, Feb. 2008.
  2. Randomized voting and A sketch of randomized voting.
    In limbo.
Talks: Here are the overheads for some of the talks I have given:
  1. Quasisymmetric expansions of cycle indices
    UGA AMS Sectional Meeting; Mar. 2016
  2. Rational Catalan numbers and the sweep map
    UVM-St. Michael's Combinatorics Seminar; Nov. 2014
  3. Rational q-Catalan numbers and q-binomials
    Halifax AMS Sectional Meeting; Oct. 2014
  4. The Sweep Map
    CMS Winter Meeting - Ottawa; Dec. 2013
  5. Quasisymmetric expansions of Schur plethysms
    Holy Cross AMS Sectional Meeting; Apr. 2011
  6. On the mu-coefficient of Kazhdan-Lusztig polynomials
    Holy Cross AMS Sectional Meeting; Apr. 2011
  7. An infinite family of partition statistics
    Penn State AMS Sectional Meeting; Oct. 2009
  8. "Statistics" in Combinatorics
    Invited talk, MathFest Aug. 2009 in Portland, OR
  9. A variation on Sylvester's four-point problem
    Gems of Combinatorics Session, MathFest Aug. 2009 in Portland, OR
  10. Combinatorial structures associated to the nabla operator
    Banff, Sep. 2007 (Jim Haglund, proxy speaker; thanks Jim!)
  11. Combinatorial aspects of nabla(s_lambda)
    given at CRM, Montreal in May 2007.
  12. Square q,t-lattice paths and nabla(p_n)
    given at FPSAC '05 in Taormina, Sicily in June 2005.
  13. Overview of Kazhdan-Lusztig Polynomials
    given at UPenn combinatorics seminar in October 2003.
  14. Counterexamples to the 0,1-Conjecture
    given at the Computational Lie Theory conference at CRM in June 2002.
  15. Maximal Singular Loci for Schubert Varieties in SL(n)/B
    given at FPSAC '01 meeting in Scottsdale, AZ in May 2001.
  16. Kazhdan-Lusztig polynomials for 321-hexagon-avoiding permutations
    given at the Joint Meeting in Washington, DC in January 2000.
Thesis: Here is my doctoral thesis.
My thesis advisor was Sara Billey at MIT (now at Univ. Washington). You can check out my mathematical genealogy at The Mathematics Genealogy Project.
Code:
  • My cyborg juggling balls.
  • Code for computing type-A Kazhdan-Lusztig polynomials. This is the code accompanying my paper Equivalence classes for the mu-coefficient of Kazhdan-Lusztig polynomials in S_n.
  • Some old code for computing type-A Kazhdan-Lusztig polynomials.
Trajectory: From F01 to S03 I was a postdoc at the University of Massachusetts at Amherst.
From F03 to S04 I was an NSF postdoctoral fellow at the University of Pennsylvania.
From F04 to F08 I was an Assistant Professor at Wake Forest University in Winston-Salem, NC.
From S09 to S14 I was an Assistant Professor at the University of Vermont in Burlington, VT.
In S14 I was promoted to Associate Professor with tenure (effective F14).