and gerrymandering
- Evaluations of gerrymandering metrics using simulated packing and cracking
In preparation. - Packed voters and cracked voters (Version 2; Aug 03, 2018)
In revision. - Accumulation charts for instant-runoff elections
Notices of the AMS, Dec. 2019
Zoomable demo of chart
Source code for interactive charts - A comparison of partisan-gerrymandering measures (Version 2; Nov 04, 2018)
code here
Elec. Law J., 18(3), 2019. - Introduction to the declination function for gerrymanders
Friendly introduction to Elec. Law J. Quantifying gerrymandering... paper. - Gerrymandering and the net number of US House seats won due to vote-distribution asymmetries (also on arXiv)
Joint with J. Buzas.
This will be split into two papers, one on simulated packing and cracking, other on Chen-Cottrell paper.
Guest post on Rick Hasen's Election Law Blog. - Quantifying gerrymandering using the vote distribution (older version on arXiv)
Election Law Journal, 17 (1)
gzipped tar file of python code used to generate data in ELJ paper
Declination in Federal district court opinion for Ohio case (Householder v. Ohio A. Philip Randolph Institute)- Other resources
- Python code to compute the declination.
- R code to compute the declination.
- Report on California Redistricting Commission by Eric McGhee utilizing the declination.
- 30-second introduction:
The declination is essentially the angle between the two black lines.
The bigger the angle, the more partisan asymmetry. Click below to enlarge.

-
Click the image for animation from 1972 to 2016
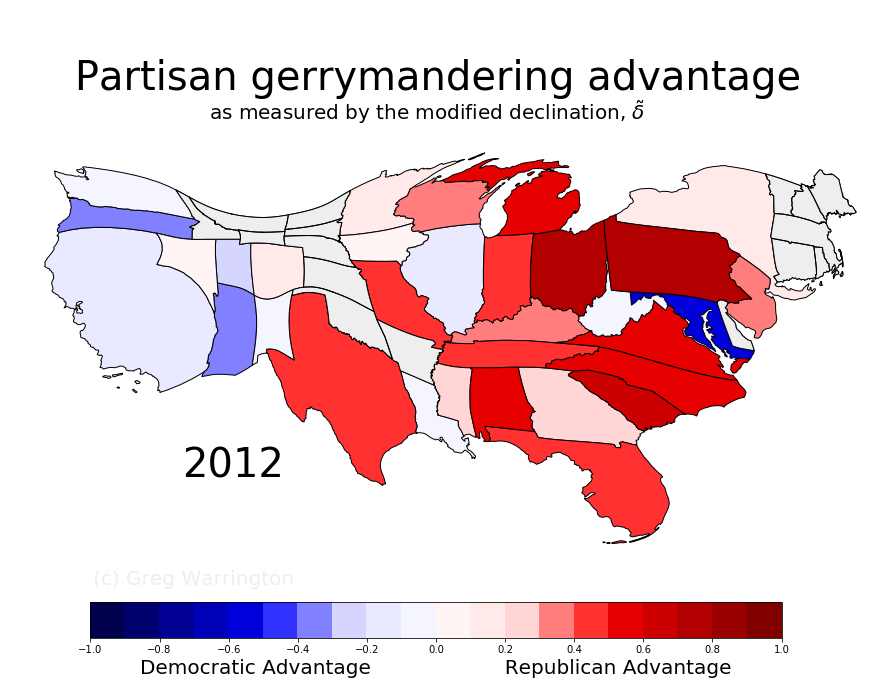
Notes on the animation:
- The cartogram adjusts state sizes according to the
number of congressional seats.
The sizes used are based on the sizes of the 2012 congressional declinations. - The version of the declination used is one (delta tilde) that is essentially independent of the number of seats.
The 2003 Texas redistricting is striking. - The cartogram adjusts state sizes according to the
number of congressional seats.
- States without at least one seat won by each party are in gray.
- Sorry Don Young and HI, you didn't fit.
- Other resources
- Abacus histories and the combinatorics of creation operators
Joint with N. Loehr.
In revision.
Python and SageMath code to accompany paper:- README
- Abacus histories (python)
- Internal representation of some linear combinations (python)
- Computations illustrated in paper (python)
- Simple file showing how a computation could be made (python)
- Some plethysm reality checks (SageMath)
- Plethystic definitions of operators (SageMath)
- Code for checking that definitions are equivalent, identities, etc. (SageMath)
- Quasisymmetric and Schur expansions of cycle index polynomials
Joint with N. Loehr.
Discrete Mathematics, 342 (1), January 2019, 113--127.
Sage worksheet for computations in the paper. also as a text file
- Orthogonal bases for transportation polytopes applied to Latin squares, magic squares and Sudoku boards
Linear Algebra Appl., 531, October 2017, 285--304.
Sage worksheet for constructing bases described in the paper.
- Sweep maps: A continuous family of sorting algorithms
Joint with D. Armstrong and N. Loehr
Sage worksheet for checking various conjectures described in the paper.
Advances in Mathematics, 284 (2015), 159-85. -
Rational parking functions and Catalan numbers
Joint with D. Armstrong and N. Loehr
Sage worksheet for checking various conjectures described in the paper.
Annals of Combinatorics, 20 (1), March 2016, 21--58. -
Shape and pattern containment of separable permutations
Joint with A. Crites and G. Panova
Ars Combinatoria, Volume CXXVIII, July, 2016, 103--116. - Martin Gardner's minimum no-three-in-a-line problem
Joint with A. Cooper, O. Pikhurko and J. Schmitt
American Mathematical Monthly, 121:3 (2014), 213-221. - Transition matrices for symmetric and quasisymmetric Hall-Littlewood polynomials
Joint with N. Loehr and L. Serrano
Journal of Combinatorial Theory, Series A, 120:8 (2013), 1996-2019.
Sage worksheet for computing various matrices described in the paper. - On the existence of three dimensional Room frames and Howell cubes
Joint with J. Dinitz and E. Lamken
Discrete Math, 313:12 (2013), 1368-1384. Find it here. - What to expect from a game of Memory
Joint with D. Velleman
American Mathematical Monthly, 120:9 (2013), 787-805. -
Quasisymmetric expansions of Schur-function plethysms
Joint with N. Loehr
Proceedings of the AMS, 140 (2012), 1159--1171. - Equivalence classes for the mu-coefficient of Kazhdan-Lusztig polynomials in S_n
Experimental Math., 20 (2011), no. 4, 457--466. - The Spectra of Certain Classes of Room Frames: The Last Cases
Joint with J. Dinitz
Elec. J. Combin. 17 (2010), no. 1, Research Paper 74, 13 pp. - From quasisymmetric expansions to Schur expansions via a modified inverse Kostka matrix
Joint with E. Egge and N. Loehr
European J. Combin. 31 (2010), no. 8, 2014--2027. - A combinatorial version of Sylvester's four-point problem
Adv. in App. Math., 45 (2010) no. 3, 390--394. - A continuous family of partition statistics equidistributed
with length
Joint with N. Loehr
J. Combin. Theory Ser. A 116 (2009), no. 2, 379--403. (final version) -
Nested quantum Dyck paths and nabla(s_lambda)
Joint with N. Loehr
International Mathematics Research Notices 2008; Vol 2008: article ID rnm157 (final version) -
Bitableaux bases for Garsia-Haiman modules of hollow type
Joint with E. Allen and M. Cox
J. Combin. Theory Ser. A 115 (2008), no. 7, 1127--1155. -
A human proof for a generalization of Shalosh B. Ekhad's 10^n Lattice Paths Theorem
Joint with N. Loehr and B. Sagan
Ars Combin. 89 (2008), 421--429. - Square q,t-lattice paths and nabla(p_n)
Joint with N. Loehr
Transactions of the AMS, 359 (2007) no. 2, 649-669.
- The combinatorics of a three-line
circulant determinant
Joint with N. Loehr and H. Wilf
Israel Journal of Mathematics 143 (2004), 141-156
- Juggling probabilities
American Mathematical Monthly 112, no. 2 (2005), 105-118
-
Counterexamples to the 0,1-Conjecture
Joint with T. McLarnan
Represent. Theory 7 (2003), 181-195 (final version)
-
A formula for inverse Kazhdan-Lusztig polynomials in S_n.
J. Comb. Theory A, Vol. 104, Iss. 2 , November (2003), 301-316 (final version)
-
Maximal singular loci for Schubert varieties in SL(n)/B.
Joint with S. Billey
Trans. AMS 355 (2003), no. 10, 3915--3945 (electronic) (final version)
-
Kazhdan-Lusztig polynomials for
321-hexagon-avoiding permuations.
Joint with S. Billey
J. of Alg. Comb., 13 (2): 111-136, March 2001 (final version)
- Urinary Buprenorphine, Norbuprenorphine and Naloxone Concentrations and Ratios
Warrington, Jill S. MD, PhD; Warrington, Gregory S. PhD; Francis-Fath, Samuel BA; Brooklyn, John MD
Journal of Addiction Medicine, ahead of print. - Use of urinary naloxone levels in a single provider practice: a case study
Jill S. Warrington, Kaitlyn Booth, (GSW), Samuel Francis-Fath
Addiction Science and Clinical Practice, 15:3, December 2020. - Predicting effects of future development on a territorial forest songbird:
methodology matters
Michelle L. Brown, Therese M. Donovan, Ruth M. Mickey, Gregory S. Warrington, W. Scott Schwenk, David M. Theobald
Landscape Ecology 33:1 (January 2018), 93-108. - Estimating landscape carrying capacity through
maximum clique analysis
Joint with Therese M. Donovan, W. Scott Schwenk and Jeffrey H. Dinitz
Ecological Applications, 22:8 (2012), 2265-2276. - A Photographic Assignment for Abstract Algebra
PRIMUS 19 (2009), no. 6, 561-564.
- Juggling Performers + Math = ?
Math Horizons, Feb. 2008.- Randomized voting and A sketch of randomized voting.
In limbo. - Randomized voting and A sketch of randomized voting.
- Quasisymmetric expansions of cycle indices
UGA AMS Sectional Meeting; Mar. 2016 - Rational Catalan numbers and the sweep map
UVM-St. Michael's Combinatorics Seminar; Nov. 2014 - Rational q-Catalan numbers and q-binomials
Halifax AMS Sectional Meeting; Oct. 2014 - The Sweep Map
CMS Winter Meeting - Ottawa; Dec. 2013 - Quasisymmetric expansions of Schur plethysms
Holy Cross AMS Sectional Meeting; Apr. 2011 - On the mu-coefficient of Kazhdan-Lusztig polynomials
Holy Cross AMS Sectional Meeting; Apr. 2011 - An infinite family of partition statistics
Penn State AMS Sectional Meeting; Oct. 2009 - "Statistics" in Combinatorics
Invited talk, MathFest Aug. 2009 in Portland, OR - A variation on Sylvester's four-point problem
Gems of Combinatorics Session, MathFest Aug. 2009 in Portland, OR - Combinatorial structures associated to the nabla operator
Banff, Sep. 2007 (Jim Haglund, proxy speaker; thanks Jim!) - Combinatorial aspects of nabla(s_lambda)
given at CRM, Montreal in May 2007. - Square q,t-lattice paths and nabla(p_n)
given at FPSAC '05 in Taormina, Sicily in June 2005. - Overview of Kazhdan-Lusztig Polynomials
given at UPenn combinatorics seminar in October 2003. - Counterexamples to the
0,1-Conjecture
given at the Computational Lie Theory conference at CRM in June 2002. - Maximal Singular Loci for Schubert Varieties in SL(n)/B
given at FPSAC '01 meeting in Scottsdale, AZ in May 2001. - Kazhdan-Lusztig
polynomials for 321-hexagon-avoiding permutations
given at the Joint Meeting in Washington, DC in January 2000.
My thesis advisor was Sara Billey at MIT (now at Univ. Washington). You can check out my mathematical genealogy at The Mathematics Genealogy Project.
- My cyborg juggling balls.
- Code for computing type-A Kazhdan-Lusztig polynomials. This is the code accompanying my paper Equivalence classes for the mu-coefficient of Kazhdan-Lusztig polynomials in S_n.
- Some old code for computing type-A Kazhdan-Lusztig polynomials.
From F03 to S04 I was an NSF postdoctoral fellow at the University of Pennsylvania.
From F04 to F08 I was an Assistant Professor at Wake Forest University in Winston-Salem, NC.
From S09 to S14 I was an Assistant Professor at the University of Vermont in Burlington, VT.
In S14 I was promoted to Associate Professor with tenure (effective F14).